|
Shripad M. Garge
Research Summary:
I work on the rationality properties of algebraic groups.
Let 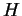 be a connected, reductive algebraic group defined over a field be a connected, reductive algebraic group defined over a field 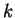 . It is natural to ask whether . It is natural to ask whether 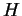 is determined by the set of is determined by the set of 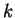 -isomorphism classes of maximal -isomorphism classes of maximal 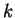 -tori in it. I studied this question over global fields, local non-archimedean
fields and finite fields. I prove following theorems in the preprint
[1]. -tori in it. I studied this question over global fields, local non-archimedean
fields and finite fields. I prove following theorems in the preprint
[1].
Theorem 1.1. Let 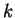 be a finite field, a global field or a local non-Archimedean field.
Let be a finite field, a global field or a local non-Archimedean field.
Let 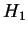 and and 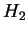 be two split, connected, reductive algebraic groups defined over be two split, connected, reductive algebraic groups defined over
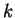 . Suppose that for every maximal . Suppose that for every maximal 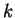 -torus -torus 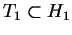 there exists a maximal there exists a maximal 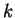 -torus -torus 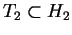 , such that the tori , such that the tori 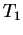 and and 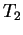 are are 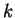 -isomorphic and vice versa. Then the Weyl groups -isomorphic and vice versa. Then the Weyl groups 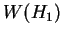 and and 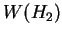 are isomorphic. are isomorphic.
Moreover, if we write the Weyl groups 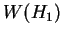 and and 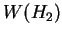 as a direct product of the Weyl groups of simple algebraic groups, as a direct product of the Weyl groups of simple algebraic groups,
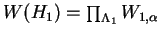 , and , and 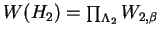 , then there exists a bijection , then there exists a bijection
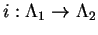 such that such that 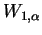 is isomorphic to is isomorphic to 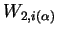 for every for every 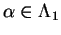 . .
Theorem 1.2. Let 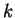 be as in the previous theorem. Let be as in the previous theorem. Let 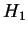 and and 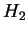 be two split, connected, semisimple algebraic groups defined over be two split, connected, semisimple algebraic groups defined over
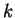 with trivial center. Write with trivial center. Write 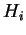 as a direct product of simple groups, as a direct product of simple groups, 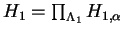 , and , and 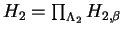 . If the groups . If the groups 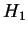 and and 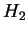 satisfy the condition given in the above theorem, then there is
a bijection satisfy the condition given in the above theorem, then there is
a bijection 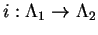 such that such that 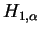 is isomorphic to is isomorphic to 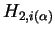 , except for the case when , except for the case when 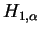 is a simple group of type is a simple group of type 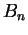 or or 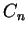 , in which case , in which case 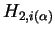 could be of type could be of type 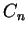 or or 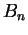 . .
My current work concerns finite groups of Lie type. It is a theorem
of Emil Artin, Tits, Kimmerle et al. that a finite simple group
is determined by its order except for the following exceptions:
I am trying to extend this theorem to the finite semisimple groups
of Lie type. Following results are expected.
- Let
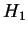 and and 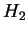 be two semisimple simply connected groups defined over finite fields be two semisimple simply connected groups defined over finite fields
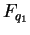 and and 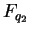 . Suppose that neither of the . Suppose that neither of the 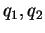 is in the set is in the set 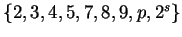 where where 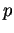 is a prime of the form is a prime of the form 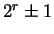 and and 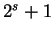 is a prime. If the order of is a prime. If the order of 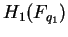 is the same as the order of is the same as the order of 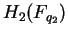 , then , then 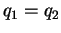 . .
- Let
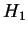 and and 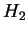 be two semisimple simply connected algebraic groups defined over
a finite field be two semisimple simply connected algebraic groups defined over
a finite field 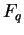 such that the order of such that the order of 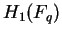 is the same as the order of is the same as the order of 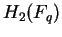 , then the orders of , then the orders of 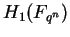 and and 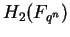 are the same for all are the same for all 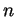 . .
I also hope to characterize the semisimple simply connected groups
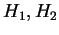 defined over a finite field defined over a finite field 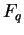 , which have exactly two simple factors and such that the
order of , which have exactly two simple factors and such that the
order of 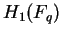 is equal to the order of is equal to the order of 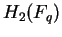 . .
Preprints:
- Maximal tori determining algebraic groups.
- On the order of finite semisimple groups (in preparation).
Conference/Workshops Attended:
- Instructional Workshop and International Conference on Geometric
Group Theory, Indian Institute of Technology, Guwahati. (December
2 - 21, 2002).
- Workshop on the Computational Aspects of Algebraic Geometry,
Harish-Chandra Research Institute, Allahabad. (January 1 - 11,
2003).
Visits to other Institutes:
- Tata Institute of Fundamental Research, Mumbai. (May 1 - July
31, 2002 and February 28 - March 28, 2003).
- Bhaskaracharya Pratishthana, Pune. (March 31 - April 15, 2003).
Invited lectures/Seminars:
- Lectured in the International Conference on Geometric Group
Theory at IIT, Guwahati, on ``Conjugacy of Weyl Groups''.
- Gave a series of lectures on ``Central Simple Algebras and the
Brauer Group'' at the Bhaskaracharya Pratishthana, Pune.
|