|
Anirban Mukhopadhyay
Research Summary:
For an integer 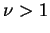 , we denote by , we denote by 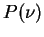 and and 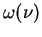 the greatest prime factor of the greatest prime factor of 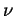 and the number of distinct prime divisors of and the number of distinct prime divisors of 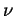 , respectively. Further we put , respectively. Further we put 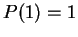 and and 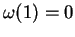 . Let . Let 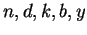 be positive integers such that be positive integers such that 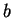 is square free, is square free, 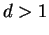 , , 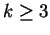 and and 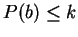 . We consider the equation . We consider the equation
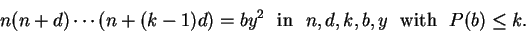 |
(1) |
Shorey and Tijdeman proved that with gcd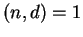 , (1) implies that , (1) implies that 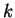 is bounded by an effectively computable number depending only on is bounded by an effectively computable number depending only on 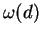 . Further Shorey showed that the assumption gcd . Further Shorey showed that the assumption gcd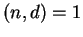 can be relaxed to can be relaxed to 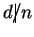 in the preceding result. On the other hand, we observe
that (1) may have infinitely many solutions in the case in the preceding result. On the other hand, we observe
that (1) may have infinitely many solutions in the case 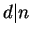 . Next Saradha and Shorey showed that (1) with . Next Saradha and Shorey showed that (1) with 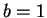 and and 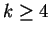 is not possible whenever is not possible whenever 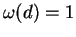 . It has also been shown by Saradha and Shorey that (1) with . It has also been shown by Saradha and Shorey that (1) with
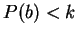 , , 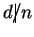 , , 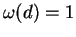 and and 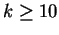 does not hold. In collaboration with T. N. Shorey I studied
(1) for does not hold. In collaboration with T. N. Shorey I studied
(1) for 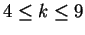 , , 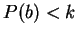 and and 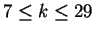 , , 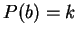 and obtained that only solution under these restrictions is and obtained that only solution under these restrictions is 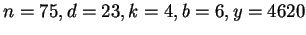 . .
Publications:
- (with Yong-Gao Chen) ; The view-obstruction problem for polygons;
Publ. Math. Debrecen 60 (2002), no. 1-2, 101-105.
- (with S. D. Adhikari and G. Coppola); On the average of the
sum-of-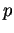 -prime-divisors function; Acta Arith. 101 (2002), no. 4, 333-338. -prime-divisors function; Acta Arith. 101 (2002), no. 4, 333-338.
Preprints:
- (with T. N. Shorey); Almost squares in arithmetic progression(II).
- (with T. N. Shorey) ; Square free part of products of consecutive
integers.
Visits to other Institutes:
Visited TIFR in February and April, 2002.
Other Activities:
Two lectures in Basic Notion seminars on ``Congruence properties
of Partition function''.
|