|
Sanoli Gun
Research Summary:
-
(with B. Ramakrishnan): Lacunarity of certain Dedekind
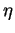 -Products. -Products.
Short Summary: A formal power series x&nu&sumn=0&infin a(n)xn is called lacunary if the arithmetic density of its non-zero coefficients is zero. Lacunarity of modular forms associated to Dedekind &eta-products is not just the pursuit of some exotic isolated theory. These have important connections with the theory of elliptic curves and modular forms. Just to cite an example, the lacunary form &eta2(4z) &eta2(8z) is nothing but the inverse Mellin transform of the Hasse-Weil L-function of the elliptic curve y2 = x3 - x. This curve plays a pivotal role in Tunnell's work on the "Congruent Number Problem".
J. -P. Serre's result [Glasgow Math. J., 27, 203--221] on all even powers of the Dedekind eta-function which are lacunary proves that the non-zero values of Ramanujan's Function &tau(n) are of arithmetic density non-zero.
B. Gordon and S. Robins [Glasgow Math. J., 37, 1--14] used Serre's method to classify all two eta products of the form &etar(z)&etas(2z), where r+s is even and rs &ne 0.
In this work, we classify all lacunary modular forms associated to the eta-products of the form &etar(z)&etas(3z), where r+s is even and rs &ne 0. As an application one gets identities for the coefficients of these lacunary modular forms.
- (with B. Ramakrishnan): On the representation of integers as sums of odd number of squares.
Short Summary: A classical problem in number theory is to give an explicit formula for the number of ways one can represent a non-negative integer n as a sum of k squares, where k is a positive integer. The study of rk(n) has a long history. A general formula for rk(n), when k is even was stated by Ramanujan . It was proved by Mordell. It is also known that rk(n) can be expressed in terms of coefficients of Eisenstein series and cusp forms. For odd values of k a general formula is not known, though formulas for particular values of k are known. For example, the formulas for rk(n) or rk(n2) are known for k = 1, 3, 5, 7, 9, 11, 13. These formulas were obtained either by an elementary method or by using the theory of modular forms. Using the Shimura Correspondence we obtain an explicit formula for r2k+1(n2), n &ge 1 . As a consequence, we prove that the values at 1-k of the Dirichlet L-functions twisted by the character &chi4 are rational and which can be written down explicitly using our formula. Here &chi4 is the trivial character or the non-trivial character modulo 4 depending on whether k is even or odd.
- (with Shaun Cooper, Michael D. Hirschhorn and B. Ramakrishnan): Multiplicative Relations for Certain Powers of Euler's Product.
Short Summary: Certain arithmetic relations for the coefficients in the expansions of (q)&infinr, (q)&infinr(qt)&infins, t=2,3,4 were studied by M. Newman, S. Cooper, M. D. Hirschhorn, R. Lewis, S. Ahlgren and R.Chapman. In this work, we prove similar identities for certain multi-product expansions using an elementary method.
- (with B. Ramakrishnan, B. Sahu and R. Thangadurai): Distribution of Quadratic non-residues which are not primitive roots.
Short Summary: In this paper we study the distribution of quadratic non-residues which are not primitive roots modulo ph or 2ph where p is an odd prime and h &ge 1 is an integer using elementary and combinatorial methods.
Conference/Workshops Attended:
- Conference on "Number Theory" in the honour of Prof. K. Ramachandra on his 70th birthday held at NIAS, Bangalore from 13th Dec. -- 15th Dec. 2003.
- Joint India-AMS Mathematical Meeting, Bangalore, India from 17th Dec. --20th Dec. 2003.
Other Activities:
- Conducted tutorial session in the VSSP programme.
|