
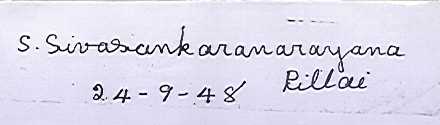
1. LIFE HISTORY OF S. S. PILLAI. On April ![]() S. Sivasankaranarayana Pillai (as S. S. Pillai - known to Mathematical community) was born at Vallam near the famous Water falls town namely Courtallam which is situated in Tirunelveli district, Tamilnadu. His parents were Subbayya Pillai and Gomati Ammal. His mother died a year after his birth. He grew up under the care of an old relative in the family. When S. S. Pillai was five years old, a master was arranged to teach Pillai at his house. At the age of nine, Pillai joined a Middle School at Shencottah. There, by looking at his high intellectual ability and his potential, a teacher called `Sastriar' gave a constant support and encouragements. Then for his Matriculation course, he moved to a local High School. During this period, he was shattered by his father's sudden death and he was struggling to continue his high school education because of monetary reasons. Fortunately, his former teacher `Sastriar' came to rescue with monetary support to complete not only to his school education but also to go beyond. He went to Nagercoil to do his Intermediate course in the Scott Christian College with a Scholarship. Then he did B. A at Trivandrum in the Maharaja's college.
S. Sivasankaranarayana Pillai (as S. S. Pillai - known to Mathematical community) was born at Vallam near the famous Water falls town namely Courtallam which is situated in Tirunelveli district, Tamilnadu. His parents were Subbayya Pillai and Gomati Ammal. His mother died a year after his birth. He grew up under the care of an old relative in the family. When S. S. Pillai was five years old, a master was arranged to teach Pillai at his house. At the age of nine, Pillai joined a Middle School at Shencottah. There, by looking at his high intellectual ability and his potential, a teacher called `Sastriar' gave a constant support and encouragements. Then for his Matriculation course, he moved to a local High School. During this period, he was shattered by his father's sudden death and he was struggling to continue his high school education because of monetary reasons. Fortunately, his former teacher `Sastriar' came to rescue with monetary support to complete not only to his school education but also to go beyond. He went to Nagercoil to do his Intermediate course in the Scott Christian College with a Scholarship. Then he did B. A at Trivandrum in the Maharaja's college.
In 1927, S. S. Pillai received a Research Studentship at the University of Madras to work under Professors K. Ananda Rao and R. Vaidyanathaswamy. Then he joined Annamalai university as a lecturer. There his mathematical achievements seem to have peaked. Indeed, Madras university honored him by awarding D. Sc. for his research achievements. He was the first one to get this honor in Mathematics. He shifted to University of Travancore in 1941. Then a year later, he joined Calcutta University as a lecturer.
For his achievements, he was invited to visit the Institute of Advance Studies, Princeton, USA for a year. Also, he was invited to participate in the International Congress of Mathematicians at Harvard University as a delegate of Madras University. So, he proceeded to USA by air in the august 1950. But due to the air crash near Cairo on August 31, 1950, Indian Mathematical Community lost one of the best known mathematicians. Of course, his mathematical works will continue to be cherished by mathematicians for all time to come.
2. SOME PEARLS FROM HIS MATHEMATICAL HISTORY. A good part of his mathematical
achievements was done in Annamalai University. He worked mostly in analytical number theory.
One of his famous contributions to the solutions of Waring' s Problem. Waring's problem states
as follows;
``Let ![]() be a given positive integer. Then
be a given positive integer. Then ![]() defined to be the smallest positive integer such that any natural number
defined to be the smallest positive integer such that any natural number ![]() can be written as sum of at most
can be written as sum of at most ![]() -
- ![]() -th powers of integers. What is the exact value of
-th powers of integers. What is the exact value of ![]() ''
''
For instance, when ![]() we have
we have ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
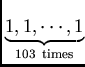
![]() squares of integers. Suppose the denominations of our currency (may be, rupee notes) in these numbers. For example, if we want to give Rs. 103 to a shop keeper, then, we can give him in the following denominations,
squares of integers. Suppose the denominations of our currency (may be, rupee notes) in these numbers. For example, if we want to give Rs. 103 to a shop keeper, then, we can give him in the following denominations,
 or
or
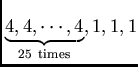 or
or
![]() or
or
![]() or
or ![]() The Warning's problem, in this case, is asking for the minimum number of denominations required to cover all the positive integers. In our example, we see that the minimum number is
The Warning's problem, in this case, is asking for the minimum number of denominations required to cover all the positive integers. In our example, we see that the minimum number is ![]() In fact, Lagrange proved that
In fact, Lagrange proved that ![]() in 1770. Note that for some integers, we can manage with fewer number of squares (that is, in stead of
in 1770. Note that for some integers, we can manage with fewer number of squares (that is, in stead of ![]() we may manage with
we may manage with ![]() or
or ![]() or
or ![]() ). For instance, we have
). For instance, we have ![]() (rather all the squares). From the work of D. Hilbert (1909) it is known that
(rather all the squares). From the work of D. Hilbert (1909) it is known that ![]() exists for every
exists for every ![]() and it is finite. Also, it is known that
and it is finite. Also, it is known that ![]()
In 1935, S. S. Pillai proved the Waring's problem for ![]() by proving that
by proving that
![]() where
where ![]() is the largest natural number
is the largest natural number ![]() Also, Pillai proved that
Also, Pillai proved that ![]() by computing, in this case, the precise value of
by computing, in this case, the precise value of ![]() as defined above. Then to complete the history of this problem
as defined above. Then to complete the history of this problem ![]() was proved by J. Chen in 1965. Then the remaining only case was
was proved by J. Chen in 1965. Then the remaining only case was ![]() and it was proved by R. Balasubramanian along with M. Deshouillers and F. Dress in 1987.
and it was proved by R. Balasubramanian along with M. Deshouillers and F. Dress in 1987.
S. S. Pillai worked on Diophantine approximations too and he proved the following beautiful theorem; ``Let ![]() and
and ![]() be natural numbers and
be natural numbers and ![]() Then for any integral
Then for any integral ![]() and
and ![]() if we have
if we have
![]() then we have
then we have
for all
S. S. Pillai gave a new proof of Bertrand's Postulate; `` Given any ![]() there is always a prime number
there is always a prime number ![]() in between
in between ![]() and
and ![]() ''. Indeed, S. Ramanujan also gave a different proof of this result. The best elementary proof known for this result is due to P. Erdos.
Below we shall list all the research publications of Pillai.
''. Indeed, S. Ramanujan also gave a different proof of this result. The best elementary proof known for this result is due to P. Erdos.
Below we shall list all the research publications of Pillai.
- On
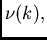 Proc. Indian Acad. Sci., IX (1935), 175 (added May, (1951)).
Proc. Indian Acad. Sci., IX (1935), 175 (added May, (1951)).
- On the equation
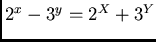 , Bull. Calcutta
Math. Soc. 37, (1945), 15-20.
, Bull. Calcutta
Math. Soc. 37, (1945), 15-20.
- Highly composite numbers of the
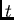 th order, J. Indian Math. Soc. (N.
S.), 8, (1944), 61-74.
th order, J. Indian Math. Soc. (N.
S.), 8, (1944), 61-74.
- Correction to my paper "Bertrand's postulate", Bull. Calcutta Math. Soc., 37, (1945), 27. Correction, Ibid, 37 (1944), 27.
- On
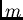 consecutive integers. IV, Bull. Calcutta Math. Soc.,
36, (1944). 99-101.
consecutive integers. IV, Bull. Calcutta Math. Soc.,
36, (1944). 99-101.
- On
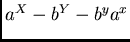 , J. Indian Math. Soc. (N. S.) 8,
(1944), 10-13.
, J. Indian Math. Soc. (N. S.) 8,
(1944), 10-13.
- On Waring's problem with powers of primes, J. Indian Math. Soc. (N.S.) 8, (1944), 18-20.
- On the smallest primitive root of a prime, J. Indian Math. Soc. (N.S.) 8, (1944), 14-17.
- Highly abundant numbers, Bull. Calcutta Math. Soc., 35, (1943), 141-156.
- Lattice points in a right-angled triangle - III, Proc. Indian Acad. Sci., Sect. A, 17, (1943), 62-65.
- Lattice points in a right-angled triangle - II, Proc. Indian Acad. Sci., Sect. A, 17, (1943), 58-61.
- On
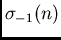 and
and 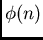 , Proc. Indian Acad. Sci.,
Sect. A, 17, (1943), 67-70.
, Proc. Indian Acad. Sci.,
Sect. A, 17, (1943), 67-70.
- On a congruence property of the divisor function, J. Indian Math. Soc. (N. S.) 6, (1942), 118-119.
- On the divisors of
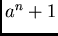 , J. Indian Math. Soc. (N. S.), 6,
(1942), 120-121.
, J. Indian Math. Soc. (N. S.), 6,
(1942), 120-121.
- On a problem in Diophantine approximation, Proc. Indian Acad. Sci., Sect. A, 15, (1942), 177-189.
- On algebraic irrationals, Proc. Indian Acad. Sci., Sect. A, 15, (1942), 173-176.
- (with George, A), On numbers of the form
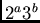 - II,
Proc. Indian Acad. Sci., Sect. A, 15, (1942), 133-134.
- II,
Proc. Indian Acad. Sci., Sect. A, 15, (1942), 133-134.
- On numbers of the form
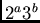 - I, Proc. Indian Acad. Sci.,
Sect. A, 15, (1942), 128-132.
- I, Proc. Indian Acad. Sci.,
Sect. A, 15, (1942), 128-132.
- Nurnberg proof of Cauchy's general principle of convergence, Math. Student, X (1942), 91-92.
- On the definition of oscillation, Math. Student, IX (1941), 165-167.
- On the sum function connected with primitive roots. Proc. Indian Acad. Sci., Sect. A, 13, (1941), 526-529.
- On
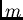 consecutive integers - III, Proc. Indian Acad. Sci., Sect. A,
13, (1941), 530-533.
consecutive integers - III, Proc. Indian Acad. Sci., Sect. A,
13, (1941), 530-533.
- On Waring's problem
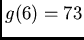 , Proc. Indian Acad. Sci., Sect. A,
12 (1940), 30-40.
, Proc. Indian Acad. Sci., Sect. A,
12 (1940), 30-40.
- On Waring's problem with powers of primes, Proc. Indian Acad. Sci., Sect. A, 12, (1940), 202-204.
- Waring's problem with indices
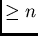 , Proc. Indian Acad. Sci.,
Sect. A, 12, (1940), 41-45.
, Proc. Indian Acad. Sci.,
Sect. A, 12, (1940), 41-45.
- A note on Gupta's previous paper, Proc. Indian Acad. Sci., Sect. A, 12, (1940), 63-64.
- On a linear Diophantine equation, Proc. Indian Acad. Sci., Sect. A, 12, (1940), 199-201.
- On normal numbers, Proc. Indian Acad. Sci., Sect. A, 12, (1940), 179-184.
- Generalisation of a theorem of Mangoldt, Proc. Indian Acad. Sci., Sect. A, 11, (1940), 13-20.
- On
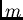 consecutive integers - II, Proc. Indian Acad. Sci., Sect. A,
11, (1940), 73-80.
consecutive integers - II, Proc. Indian Acad. Sci., Sect. A,
11, (1940), 73-80.
- On
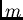 consecutive integers - I, Proc. Indian Acad. Sci., Sect. A,
11, (1940), 6-12.
consecutive integers - I, Proc. Indian Acad. Sci., Sect. A,
11, (1940), 6-12.
- On the converse of Fermat's theorem, Math. Student, VIII (1940), 132-133.
- Symposium on Waring's problem, Chairman's address, Math. Student, VII (1939), 165-168.
- On Stirling's approximation, Math. Student, VII (1939), 70-71.
- On Waring's problem, IX (on universal Waring's problem with prime powers), Jour. Indian Math. Soc., N. S. III (1939), 221-225.
- On Waring's problem, VIII (with polynomial summonds), Jour. Indian Math. Soc., N. S. III (1939), 205-220.
- On numbers which are not multiples of any other in the set, Proc. Indian Acad. Sci., Sect. A, 10, (1939), 392-394.
- On the number of representations of a number as the sum of the square of a prime and a squarefree integer, Proc. Indian Acad. Sci., Sect. A, 10, (1939), 390-391.
- A note on the paper of Sambasiva Rao, J. Indian Math. Soc. 3, (1939), 266-267.
- On the smallest prime of the form
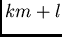 , Proc. Indian Acad. Sci.,
Sect. A. 10, (1939). 388-389.
, Proc. Indian Acad. Sci.,
Sect. A. 10, (1939). 388-389.
- On normal numbers. Proc. Indian Acad. Sci., Sect. A. 10, (1939), 13-15.
- On Waring's problem with powers of primes, Proc. Indian Acad. Sci., IX (1939), 29-34.
- On the addition of residue classes, Proc. Indian Acad. Sci., VII (1938), 1-4.
- Generalization of a theorem of Davenport on the addition of residue classes, Proc. Indian Acad. Sci., VI (1937), 179-180.
- On Waring's problem VI, Annamalai University Journal, (1937), 171-197.
- (with S. Chowla), The number of representations of a number as a sum of
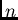 non-negative
non-negative 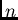 th powers, Quart. J. Math. Oxford Ser., 7 (1936), 56-59.
th powers, Quart. J. Math. Oxford Ser., 7 (1936), 56-59.
- (with S. Chowla), Hypothesis K of Hardy and Littlewood, Math. Z., 41 (1936), 537-540.
- On Waring's problem V : on
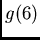 , Jour. Indian Math. Soc., New series, II (1936), 213-214.
, Jour. Indian Math. Soc., New series, II (1936), 213-214.
- On
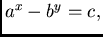 Jour. Indian Math. Soc., New series, II (1936), 119-122. Correction, Ibid, p, 215.
Jour. Indian Math. Soc., New series, II (1936), 119-122. Correction, Ibid, p, 215.
- On the set of square free numbers, Jour. Indian Math. Soc., New series, II (1936), 116-118.
- On Waring's problem II, Jour. Indian Math. Soc., New series, II (1936), 16-44.
- On Waring's problem IV, Annamalai University Journal, VI, 1 (1936), 54-64.
- On Waring's problem III, Annamalai University Journal, VI, 1 (1936), 50-53.
- On Waring's problem I, Annamalai University Journal, V, 2 (1935), 145-166.
- Periodic simple continued fractions, Annamalai University Journal, IV, 2, (1935), 216-225.
- On the nature of conduct of conics
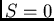 and
and
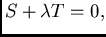 Math. Student, III (1935), 156.
Math. Student, III (1935), 156.
- Remarks on Dr. Moessner's paper, Math. Student, II (1934), 104-106.
- On a passtime common among South Indian school children, Math. Student, I (1933), 52-56.
- On an arithmetic function, Annamalai University Journal, II, 2 (1933), 242-248.
- On the sum function of the number of prime factors of
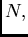 J. Indian Math. Soc., XX (1931), 70-87.
J. Indian Math. Soc., XX (1931), 70-87.
- On an arithmetic function concerning primes, Annamalai University Journal, I, 2 (1932), 1-9.
- On the indeterminant equation
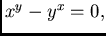 Annamalai University Journal, I, 1 (1932), 59-61.
Annamalai University Journal, I, 1 (1932), 59-61.
- An old result concerning
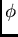 function, J. Indian Math. Soc., XIX (1931), 165-168.
function, J. Indian Math. Soc., XIX (1931), 165-168.
- (with S. Chowla), Periodic simple continued fractions, J. London. Math. Soc., 6 (1931), 85-89.
- On the inequality
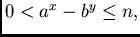 J. Indian Math. Soc., XIX (1931), 1-11.
J. Indian Math. Soc., XIX (1931), 1-11.
- On some Diophantine equations, J. Indian Math. Soc., XVIII (1930), 291-295.
- On a function analogues to
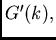 J. Indian Math. Soc., XVIII (1930), 289-290.
J. Indian Math. Soc., XVIII (1930), 289-290.
- On the numbers which contain no prime factors of the form
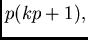 J. Indian Math. Soc., XVIII (1930), 51-57.
J. Indian Math. Soc., XVIII (1930), 51-57.
- (with S. Chowla), On the error tems in some asymptotic formulae in the theory of numbers - II, J. Indian. Math. Soc., 18 (1930), 181-184.
- (with S. Chowla), On the error tems in some asymptotic formulae in the theory of numbers - II, J. London. Math. Soc., 5 (1930), 95-101.
- A theorem concerning the primitive periods of integer matrices, J. London Math. Soc., 4 (1929), 250-251.
- On the representation of a number as the sum of two positive powers, J. London Math. Soc., 3 (1928), 56-61.
- On a function connected with
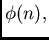 Bull. Amer. Math. Soc., XXXV (1929),
837-841.
Bull. Amer. Math. Soc., XXXV (1929),
837-841.
- On some functions connected with
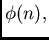 Bull. Amer. Math. Soc., XXXV (1929), 832-836.
Bull. Amer. Math. Soc., XXXV (1929), 832-836.
- On some empirical theorems of Scherk, J. Indian Math. Soc., XVII (1927-28), 164-171.
- A test for groups of primes, J. Indian Math. Soc., XVII (1927-28), 85-88.
2) S. Raghavan, Outstanding Indian Mathematician - Dr. S. S. Pillai, Ramanujan News letters, (2001)
| BACK TO MY HOMEPAGE |